3.1 No Objects
It’s just a category with no objects and no morphism.
3.2 Simple Graphs
A category can be made from a directed graph as long as the rules in 1. Category is fulfilled.
3.3 Orders
We may have an order in a category. In fact, a category may have orders as the morphism itself!
A category that may have a ranking between objects, where the ranking is composable (i.e. if and then ), and that has an identity function (i.e. ) is called a preorder.
A preorder that states if and holds, then must be is called a partial order.
A partial order in which every pair of objects must be comparable is called a total order.
3.4 Monoid as Set
A monoid in set theory requires 3 things: a set of anything, an associative binary operation, and an element in that set that behave like an identity.
e.g. Set of natural numbers (with 0) and addition as the operation.
3.5 Monoid as Category
Remember that Integer can be seen as a set in a Set category? We can then see binary operation on the Integer as a morphism from an object into itself.
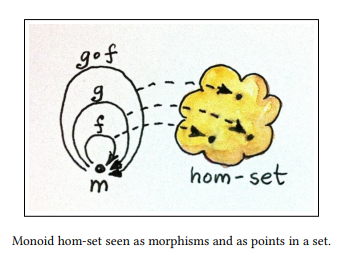
Wait, musn’t morphism in a category be composable? Well, it actually holds true here!
For example, we can compose a function that adds a number by 5, and a function that adds a number by 7 to get a function that adds number by 12.
Also! Turns out we can extract the set of morphisms here, that is, the Hom-Set . Note that an element of the hom-set can also be seen as a morphism in a category.
Next: 4. Kleisli Categories