5. Product and Coproducts

5.1 Initial Object

Initial object is an object with one and only one (not more not less) morphism going to any object in the category.

Since every initial objects have the same amount of morphism to same type of objects, every initial objects can be seen as Unique Up to Isomorphism.

An example would be Void type in Haskell, which was explained in 2. Types and Functions.

5.2 Terminal Object

The terminal object is the object with one and only one morphism coming to it from any object in the category.

Like initial objects, every terminal objects can be seen as Unique Up to Isomorphism.

An example would be the () type in Haskell in something like unit :: a -> ()

5.3 Duality

You’ve probably noticed that initial and terminal object are pretty similar, just differing in direction. It turns out that for any category, we can define an opposite category $C^{op}$ just by reversing all of the arrows. This is automatically classified as a valid category (you can try and see why).

5.4 Isomorphism

The idea is explained in Unique Up to Isomorphism. An isomorphism is an invertible morphism; or a pair of morphisms, one being the inverse of the other.

Morphism $g$ is the inverse of morphism $f$ if their composition is the identity morphism, or

$f.g=id$

$g.f=id$

Look at the following graph of two initial objects.

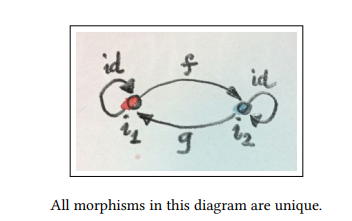
We can easily see that the equation above holds true in the image.

Another thing to notice is that $f$ and $g$ are unique, meaning that there could be more than one isomorphism between these two, but not here. Meaning, that it is not only Unique Up to Isomorphism, but also unique up to unique isomorphism.

5.5 Products

Proper definition: A product of two objects $a$ and $b$ is the object $c$ equipped with two projections such that for any other object $c’$ equipped with two projections there is a unique morphism $m$ from $c’$ to $c$ that factorizes those projections.

Whaaaaat does that even mean?

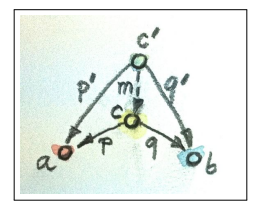
Explained by the picture above, it (kind of) means that a product $c$ is a representation that’s most sufficient on representing $a$ and $b$ such that any other representation with transformation to $a$ and $b$ can also be transformed to $c$ first and then to $a$ and $b$.

Example: $pair(a,b)$ is the product of $a$ and $b$ as it’s the most sufficient one to represent them both.

5.6 Coproduct

Product also has a 5.3 Duality, called the coproduct. First, proper definition: A coproduct of two objects $a$ and $b$ is the object $c$ equipped with two injections such that for any other object $c’$ equipped with two injections there is a unique morphism $m$ from $c$ to $c’$ that factorizes those injections

Let’s flip the graph from before.

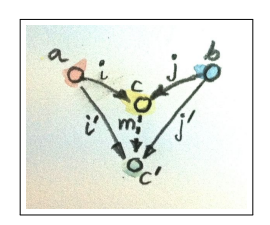
You probably get the gist already. A coproduct is kind of the object $c$ that can be obtained from either* (choose one) a or b that can be transformed further into $c^{\prime }$ through $m$. It’s basically a disjoint union. In Haskell, a union data type can be called Either, which is defined as Either a b = Left a | Right b

Next: 6. Simple Algebracic Data Types